Author:
(1) Sharif Elcott, equal contribution of Google Japan (Email: [email protected]);
(2) J.P. Lewis, equal contribution of Google Research USA (Email: [email protected]);
(3) Nori Kanazawa, Google Research USA (Email: [email protected]);
(4) Christoph Bregler, Google Research USA (Email: [email protected]).
Table of Links
- Abstract and Introduction
- Background and Related Work
- Method
- Results and Failure Cases
- Limitations and Conclusion, Acknowledgements and References
3 METHOD
Our method starts with a DIP network to reconstruct the target image. A second output head is added and tasked with inpainting the desired alpha in the trimap unknown region, constrained by the values in known regions. The main idea is that the first output head forces the network representation preceding it to "understand the structure of the image," while the second output head makes use of that information in estimating the matte.
In addition to the alpha output we add two additional networks which simultaneously reconstruct the foreground and background. Similarly to the first output of the first network, these networks’ outputs are constrained to match the target image but, unlike the first network, they are constrained only in their respective regions of the trimap. Similarly to the alpha output, they extrapolate those constraints to inpaint the unconstrained region (see Fig. 2).
The latter three outputs – 𝛼,ˆ 𝐹,ˆ 𝐵ˆ – are coupled via an additional constraint that they together satisfy (1) (see Detailed Loss below).
We put 𝐹ˆ and 𝐵ˆ in separate networks (as in [Gandelsman et al. 2019]) rather than as additional outputs heads of the first network (as in [Sun et al. 2021]) in order to allow the inpainting of the foreground to be independent of the background. All three networks share the same generic U-net structure [Ulyanov et al. 2018], except for an additional output head in the first network. Our experiments use Adam [Kingma and Ba 2015] with a learning rate of 0.001.
3.1 Detailed Loss
The first term of our loss function is the reconstruction loss between the first network output and the target image:
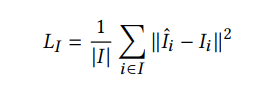
The second loss term constrains 𝛼ˆ,
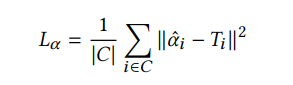
where 𝑇 is the trimap and 𝐶 = 𝐹 ∪ 𝐵 is the constrained region of the trimap.
The reconstruction losses for the foreground and background outputs are defined similarly to 𝐿𝐼 , but constrained only in their respective regions of the trimap:
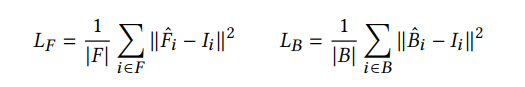
The three networks’ outputs are coupled via the alpha-compositing equation as follows:
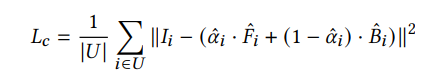
where 𝑈 = 𝐼 − 𝐶 is the unconstrained region of the trimap.
Finally, we include an exclusion loss similar to [Sun et al. 2021] to prevent the structure of the foreground from leaking into the background and vice-versa:
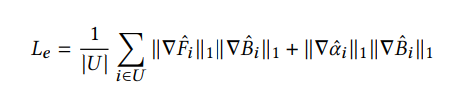
The total loss is the sum of the above six components:
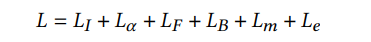
Unlike other DIP-based techniques, our algorithm does not require early stopping since the goal is to exactly fit both the image and the trimap constraints.

3.2 Temporal continuity
In our experiments temporal continuity was obtained by warmstarting the optimization for frames other than the first with the final weight values of the previous frame, and stopping with a loss threshold rather than a fixed number of iterations (see video). This simple strategy produces reasonable results even on the relatively difficult case of hair. It also reduces the compute time by roughly an order of magnitude.
3.3 Why does it work?
The deep image prior empirically demonstrates that standard convolutional networks can act as a good low-level prior for image reconstruction tasks, but why can it be adapted to invent plausible alpha mattes? Our intuition is as follows: The DIP provides a somewhat deep and hierarchical encoding of the particular image. The features in this encoding will primarily span valid image structures, with noise lying outside this space. In our work these features are re-combined to produce the matte. This works because the alpha matte contains structures that relate to those in the foreground image. In this respect our approach resembles a "deep" version of the guided image filter [He et al. 2010].
This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.

